開發者指南：透過 Swift 重新認識Accelerate Framework

iOS SDK中隱藏的幾個沒有被充分利用和不太受歡迎的框架，但其中有一些可以是相當實用且省時的工具，Accelerate Framework就是其中一個，它可用於Swift和Obj-C，Accelerate Framework讓開發人員在大規模的數學和圖像計算工作上更容易，優化任務處理的性能，因此，它廣泛應用於機器學習的領域。該框架包含用於向量和矩陣數學、數位信號處理、大量處理和圖像處理的各種C API。如果這聽起來很複雜，別擔心。你不需要知道很多數學，只要你明白這些概念。

首先，我們來到Xcode並創建一個新的playground，可以命名為任何你想要的名稱，並將平台設置為macOS，創建playground之後，請選擇所有內容並將其刪除，這樣就可以有一個乾淨的工作，在這個playground頂部請輸入以下內容來import下列這些函式庫。

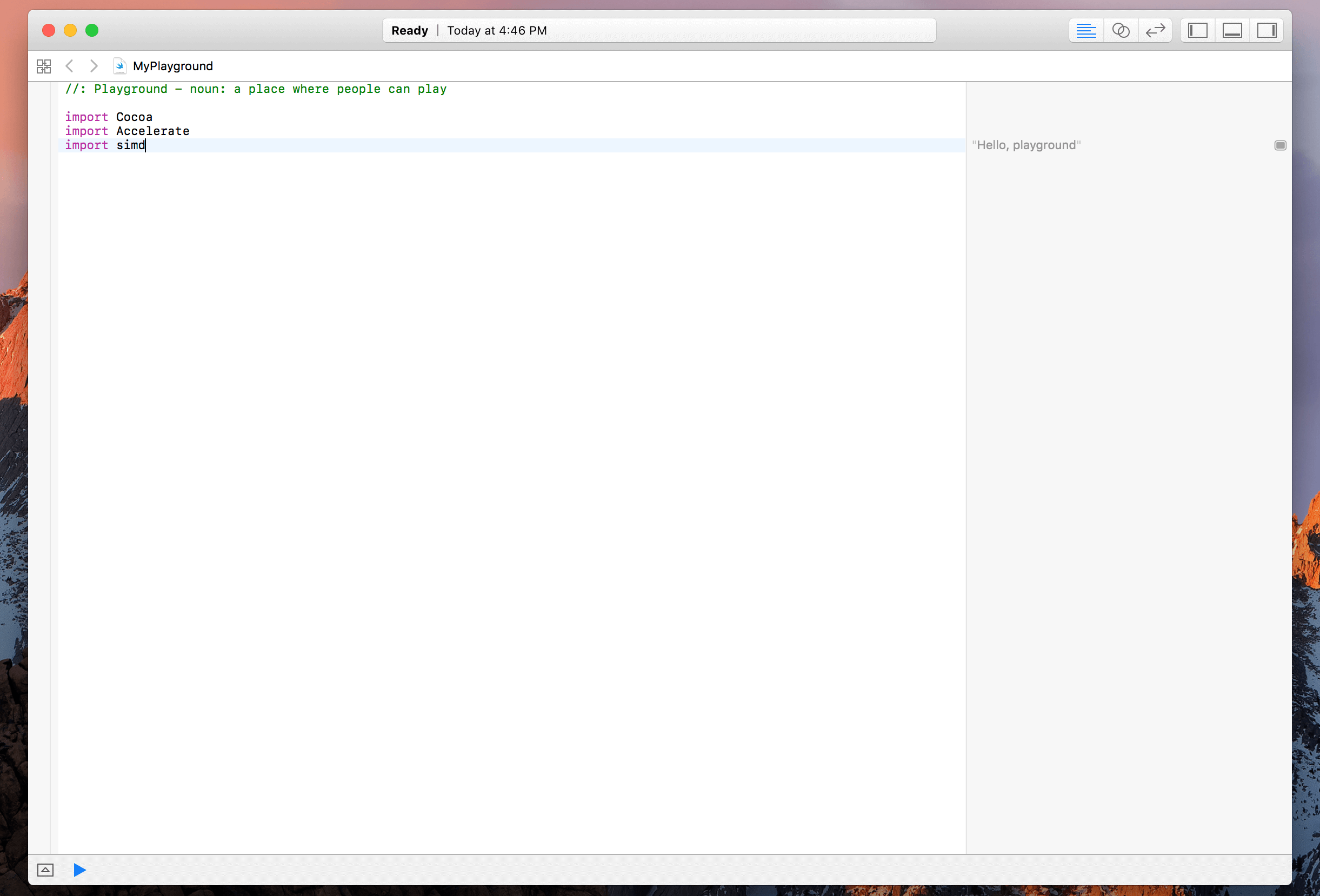
import Cocoa
import Accelerate
import simd

現在我們準備開始用Accelerate框架編寫程式碼了！

BLAS（Basic Linear Algebra Subroutines：基本線性代數子程序）

<在第一個例子中，我們將討論如何解決一個常見的線性代數方程式：

Ax + y

其中”A”是常數，x和y是一個矩陣。如果你不知道什麼是矩陣或向量也不用擔心，矩陣基本上是數組，行數是1或列數是1的矩陣又可分別稱為行向量和列向量，所以開始前，首先我們需要定義我們的向量。

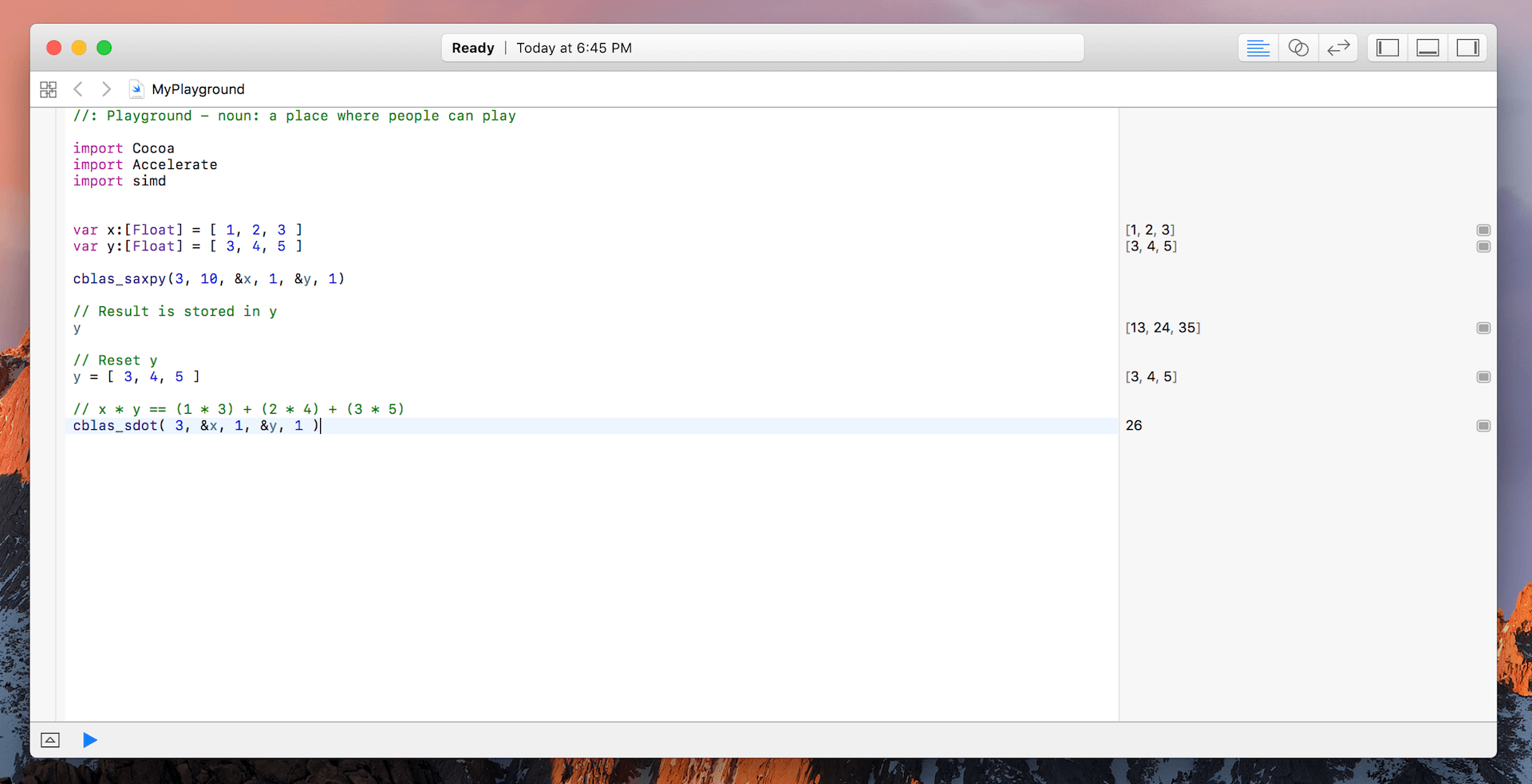
var x:[Float] = [ 1, 2, 3 ]
var y:[Float] = [ 3, 4, 5 ]

在上面的代碼中，我們定義了我們的向量x和y，分別為數字 1，2，3 和 3，4，5 的數組，有了向量x和y，現在來定義的常數，在這個例子中，我決定使用10，但你可以使用任何數字，接下來，我們要計算一下：

10x + y

現在複製下面給的函式。

cblas_saxpy(3, 10, &x, 1, &y, 1)

cblas_saxpy(_:_:_:_:_:_:)是一個函式，它計算一個常數乘以一個向量加一個向量，這正是我們想要的。參數定義（按順序）：

• 向量中的元素個數
• 常數A
• “x”向量
• “x”向量中的stride(兩個元素的距離)
• “y”向量
• “y”向量中的stride。

在第二個例子中，我們將使用內積乘以向量：

∑a[i] * b[i]

我們將使用與前面範例相同的向量，把y重新設置為原來的樣子，然後我們將使用函數cblas_sdot(_:_:_:_:_:)乘以兩個向量。

y = [ 3, 4, 5 ]

// x * y == (1 * 3) + (2 * 4) + (3 * 5)
cblas_sdot( 3, &x, 1, &y, 1 )

該函數的參數類似於cblas_saxpy(_:_:_:_:_:_:)函數，唯一的區別是，由於我們乘以2個向量，所以不存在常數的參數，對於BLAS函式庫中的更多功能，讀者有興趣可以查看此處。

LAPACK (Linear Algebra Package：線性代數套件)

LAPACK並不是一個由Apple發行Accelerate framework內的標準函式庫，但Swift支援它，這是一個好消息，因為LAPACK有很多優點，在下一個例子中，我們將解決聯立方程式，要解決的3個方程式如下：

1. 7x+5y-3z = 16
2. 3x-5y+2z= -8
3. 5x+3y-7z= 0

將以下程式碼複製到你的playground。

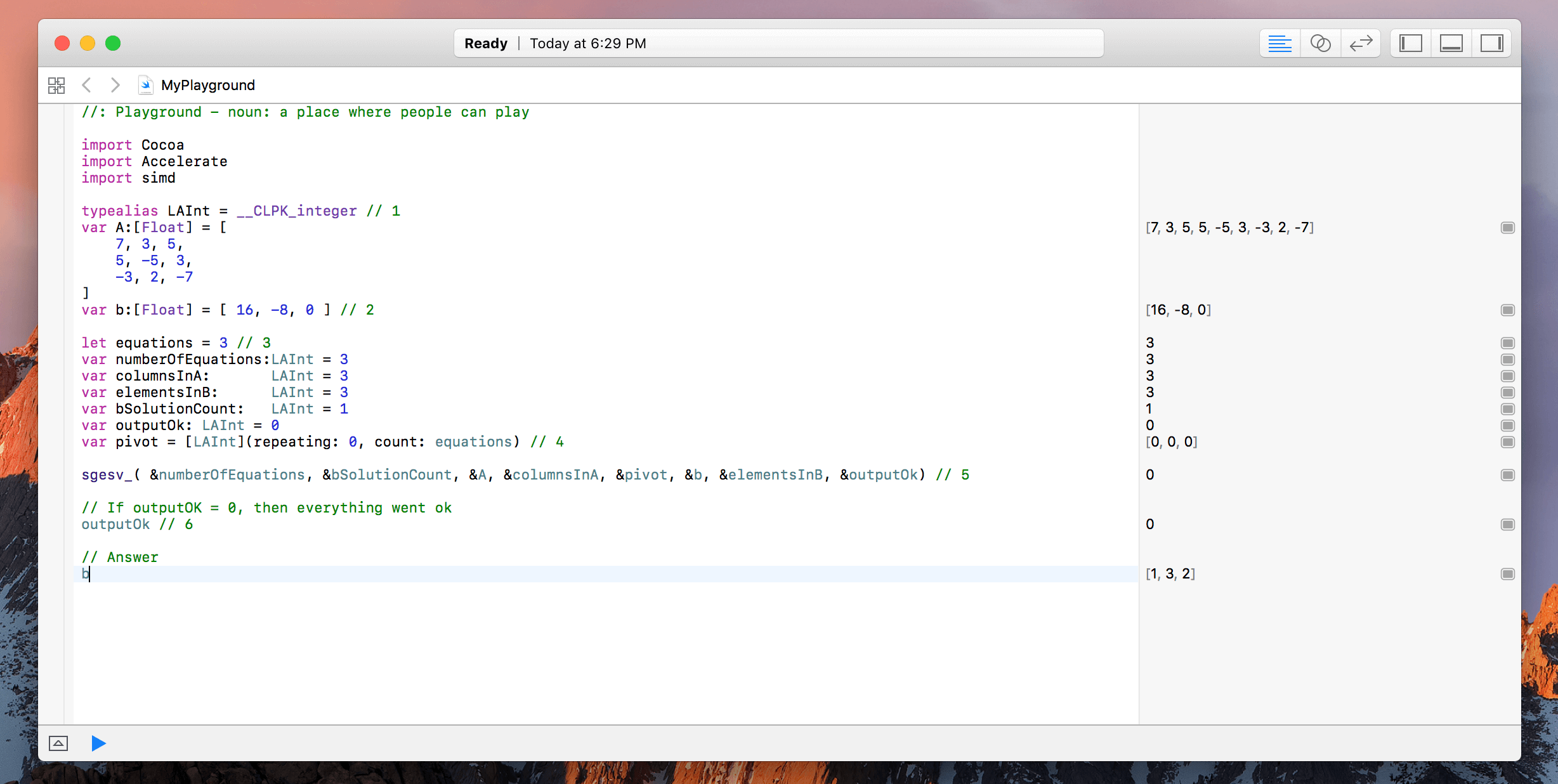
typealias LAInt = __CLPK_integer 
var A:[Float] = [
    7, 3, 5,
    5, -5, 3,
    -3, 2, -7
]
var b:[Float] = [ 16, -8, 0 ]

let equations = 3 
var numberOfEquations:LAInt = 3
var columnsInA:       LAInt = 3
var elementsInB:      LAInt = 3
var bSolutionCount:   LAInt = 1 
var outputOk: LAInt = 0
var pivot = [LAInt](repeating: 0, count: equations)

sgesv_( &numberOfEquations, &bSolutionCount, &A, &columnsInA, &pivot, &b, &elementsInB, &outputOk)

// If outputOK = 0, then everything went ok
outputOk

// Answer
b

我們來看看程式碼，結果會出現什麼。

• 第1行:我們正在使用以下等式定義一個LAInt類型。
• 第7行:現在，我們定義矩陣A和向量B，它將保存我們聯立方程式中的常數。(矩陣A將存放方程式左側的常數，向量B將存放方程式右側的常數)
• 第9行:我們定義要解決的聯立方程式個數。
• 第15行:現在，我們定義了一些變量，這些變量將被放入sgesv_(_:_:_:_:_:_:_:_:)子程式的參數中。
• 第17行:我們執行sgesv子程式。參數定義（按順序）：求解線性方程的數量，向量B中的列數，矩陣A係數，矩陣A中的列，置換矩陣，向量B係數，向量B中的列元素，和outputOK。
• 第20行:確定此變量計算是否正常。如果outputOk = 0，則計算成功，否則方程式不能被解決。

如果所有的計算都正確，那麼當輸入b時，輸出應該是[1，3，2]，這些是x，y和z的解答。

simd (Single Instruction Multiple Data:單指令多數據)

simd也是Accelerate框架之外的另一個函式庫，它能與Swift兼容，這個函式庫簡化了許多數學計算，還記得BLAS第一個例子？我們必須使用cblas_saxpy（_：_：_：_：_：_：）函式，其實，這邊有一個更簡單的方法來執行計算：

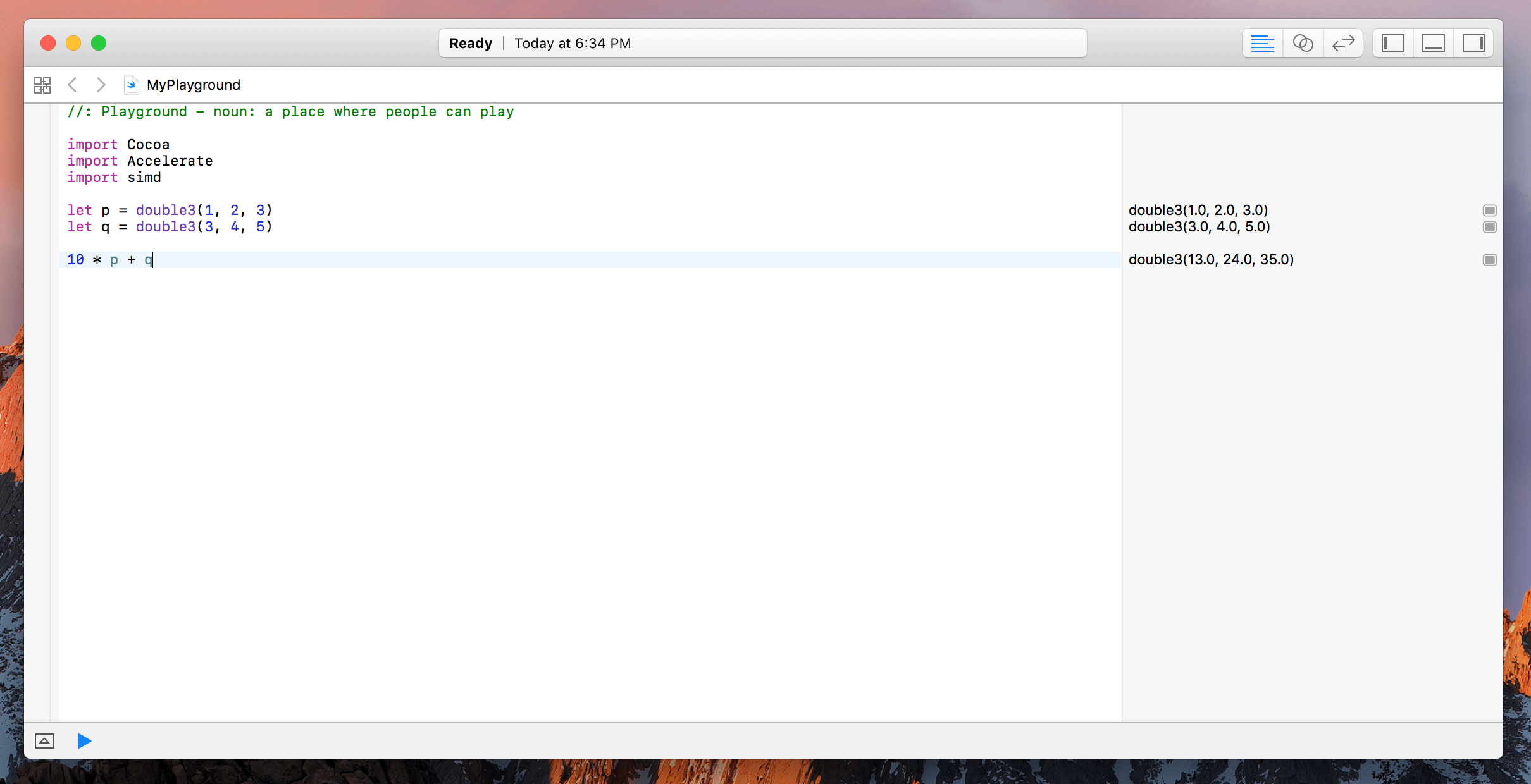
10 * x + y

為了避免變量的重疊，我們來將x、y轉變為p、q。首先，通過定義向量p和q來完成。

let p = double3(1, 2, 3)
let q = double3(3, 4, 5)

現在….神奇的事情發生了:

10 * p + q

就這樣而已！這比使用cblas_saxpy（_：_：_：_：_：_：）容易得多，雖然這個例子比較簡單，但simd更常用於2D，3D和4D數學和幾何，它也適合與其他函式庫搭配使用，如ModelIO、SpriteKit、Metal等。但是，由於這些數學過於複雜，所以本篇教程中不會碰到。

vecLib

vecLib是一個函式庫，它包含可以抽象向量處理函式庫的函數，如果你在應用程序中使用向量指令，建議你使用這些功能，以便程式碼可以輸出到不同的CPU架構，我們從複製以下代碼開始，我們只需要定義一個創建Float數組的函數：

func floats(_ n: Int32) -> [Float] {
    return [Float](repeatElement(0, count: Int(n)))
}

在第一個例子中，我們將計算一個向量的絕對值。例如，如果我定義了一個向量A = [-3，-2，-5，-10]，則通過該函數後，向量應該讀取[3，2，5，10]，我們將用於完成此計算的函數是vvfabsf(_:_:_:)。

現在首先要做的是定義參數，我們需要的參數有一個包含每個集合中的元素個數的整數、一個input array和一個output array。

var count: Int32 = 4
var aAbsolute = floats(count)
var a:[Float] = [-3, -2, -5, -10]

我們已經定義完參數了，現在只剩下一件事了：將參數插進函式中!

vvfabsf(&aAbsolute, &a, &count)
aAbsolute

如果一切正常，你得到的輸出結果應該會是[3，2，5，10]！

在第二個例子中，我們將使用vvintf(_:_:_:)函式截斷向量中的數字，將程式碼複製並貼到你的playground裡面：

count = 3
var f:[Float] = [3.3796, 1.8036, -2.1205]
var bInt = floats(count)

vvintf(&bInt, &f, &count)
bInt

與前面的例子類似，我們首先定義vvfabsf函式所需的參數。然後，我們只需要將它們插入該函式裡面。

現在這邊給讀者一個小挑戰！看你能否通過使用vvsqrtf(_:_:_:) 函式並定義參數，可以將16,9,4和1放在一個向量中，然後找到它們的平方根？

希望讀者都能夠完成挑戰！但是如果你無法完成也不用擔心！這是比較進階的東西，如果你第一次嘗試無法順利解題也沒關係。
下列程式碼就是如何找到16,9,4和1平方根的方法。

count = 4
var c:[Float] = [16,9,4,1]
var cSquareRoots = floats(count)

vvsqrtf(&cSquareRoots, &c, &count)
cSquareRoots

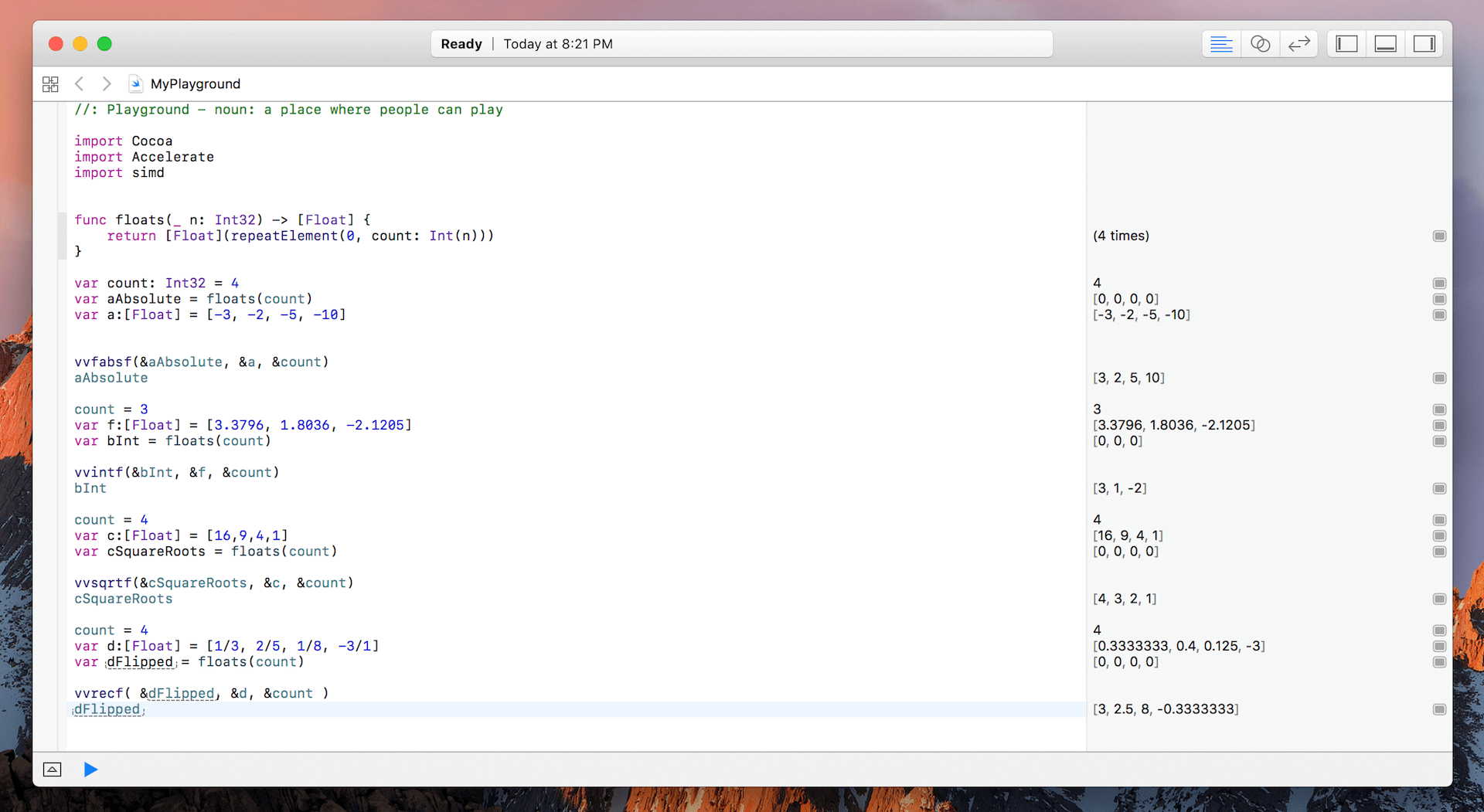
cSquareRoots的輸出應為[4，3，2，1]。

接著來介紹vecLib的最後一個例子：如果採用vvrecf(_:_:_:)這個逆向轉換函式，看看你能否針對一個包含四個分數[1/3, 2/5, 1/8, -3/1]的向量，將其中元素的分子與分母交換後轉為新的數值？參數與前面的例子相同。

希望讀者都能順利完成這個範例，這個例子的程式碼如下：

count = 4
var d:[Float] = [1/3, 2/5, 1/8, -3/1]
var dFlipped = floats(count)

vvrecf( &dFlipped, &d, &count )
dFlipped

這四個例子只是快速瀏覽在開發應用程序中使用vecLib的可能性，還有更多的函式可以用來完成你的數學計算需求。有關vecLib函式庫中可用的更多功能和子程式，請查看Apple Developer的官方vecLib文檔。

vDSP

vDSP是一個支援C和Swift API的函式庫，用在單一向量執行常用的程序，與先前的函式庫類似，讀者可以使用此函式庫執行矩陣和向量算術…但我認為那些已經足夠了，所以讓我們嘗試一下不同的東西，假設你有一組描述路徑的點，我們每一步離起點有多遠？使用vDSP解決這個問題非常簡單，因為我們在vDSP函式庫中有幾個計算距離功能！

我們首先在NSBezierPath上定義幾個點。

var points:[CGPoint] = [
    CGPoint(x: 0, y: 0),
    CGPoint(x: 0, y: 10),
    CGPoint(x: 0, y: 20),
    CGPoint(x: 0, y: 30),
    CGPoint(x: 0, y: 40),
    CGPoint(x: 0, y: 50),
    CGPoint(x: 0, y: 60),
    CGPoint(x: 0, y: 70),
    CGPoint(x: 0, y: 80)
]

let path = NSBezierPath()
path.move(to: points[0])

// IMP: Remove the space between the < and points
for i in 1..< points.count {
    path.line(to: points[i])
}

請注意我們的點全部聚焦在y軸上。如此一來，在以後仔細驗證計算時，對我們來說會更容易。現在，我們將用於計算距離的函數是vDSP_vdist(_:_:_:_:_:_:_:)。參數定義：x值，x的stride，y值，y的stride，輸出向量結果，輸出向量結果的stride以及要處理元素的數量。

var xs = points.flatMap { Float($0.x) }
var ys = points.flatMap { Float($0.y) }
var distance = [Float](repeating: 0, count: points.count)

vDSP_vdist(&xs, 1, &ys, 1, &distance, 1, vDSP_Length(points.count))
distance.map { $0 }

現在，很難確認我們是對的...但是請忍受一下，如果你注意一下上列各個點，會發現每個點都是用前一個點添加10做為下一個點。所以按照升序規則，我們的距離是10,20,30 ...等等。 因此，由於我們增加相同的常數，如果繪製這些點，將得到一個線性圖。如果在輸出控制台中點擊(10 times)旁邊的小眼睛圖標，應該出現看到下圖結果。

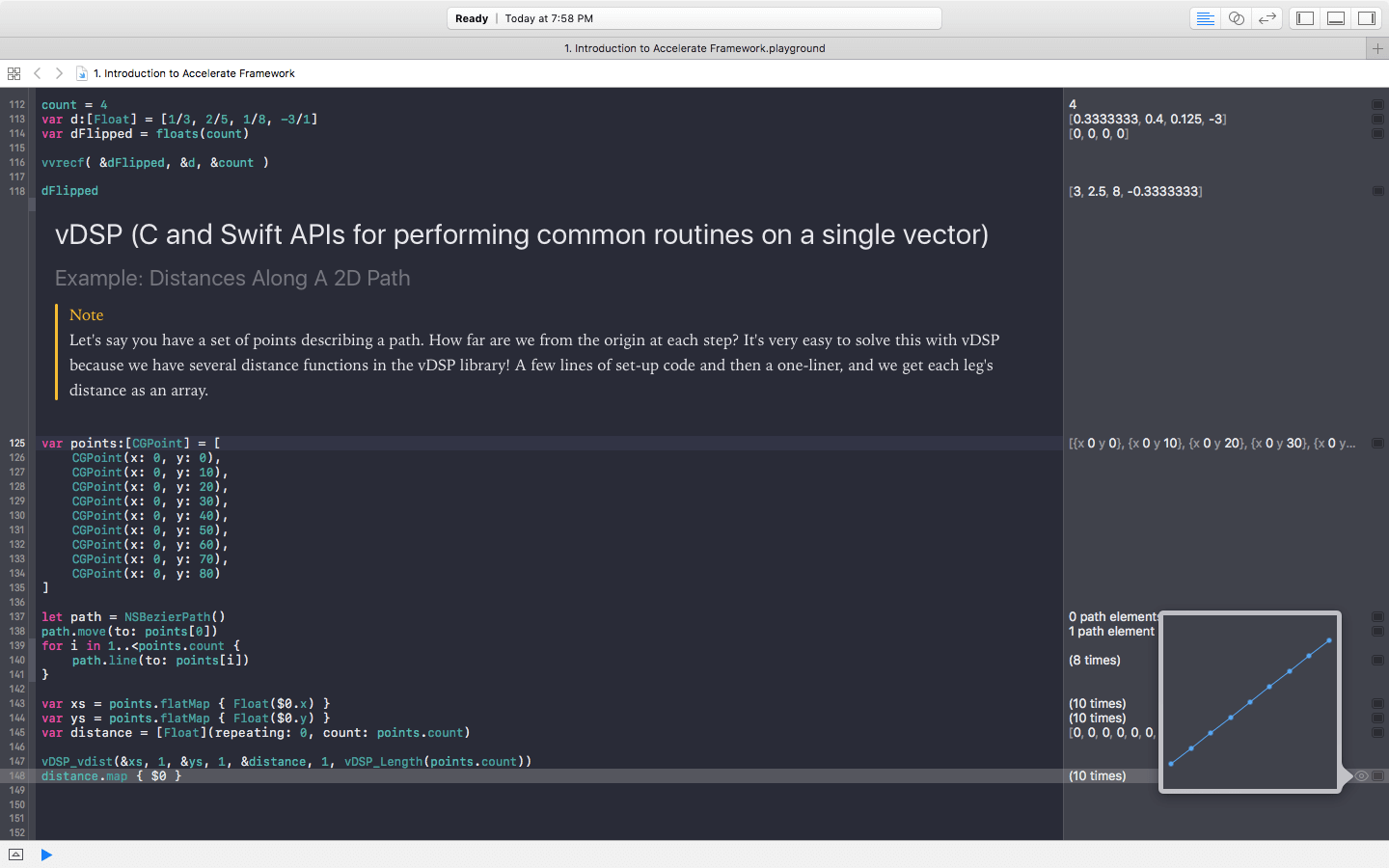
如果我們想計算出移動的全部距離怎麼辦？只需要計算10 + 20 + 30 + blah blah blah，我們是軟體工程師...不會想耗神逐一計算到80。我們可以透過程式碼，讓電腦幫我們完成這些事，並給我們正確的輸出結果，要計算總距離，只需輸入以下程式碼。

distance.reduce(0, +)

就這麼簡單！你應該會看到360這個輸出數值。

總結

這就是本教程中關於Accelerate的所有內容，這是該框架中大部分的數學計算。還有兩個更重要的函式庫：BNNS (Basic Neural Network Subroutines：基本神經網絡子程序)和vImage（圖像上的向量計算）。但是，如果我在本教程中介紹它們，那篇幅可能會太過冗長。此外，我認為我們今天已經學習到足夠的數學，其他的函式庫待下一次再來研究。

以供參考，你可以在GitHub下載完整的Xcode playground檔案。

有關Accelerate框架的更多詳細資訊，可以參考Accelerate官方文檔。